In Machine Learning, an error is an important measure of how accurately our model can predict on data that it uses to learn as well as how it behaves with new and unseen data. Based on the error, we tend to choose the machine learning model which would produce the best performance on a particular dataset. In this article, we will be discussing one such problem in machine learning models known as the Bias-Variance Tradeoff. We will try to explore what it is and how one can overcome it. Below is the outline of important points that we will cover in this article.
Table Of Contents
- What is Bias?
- What is Variance?
- The Bias-Variance Tradeoff
- How to overcome Bias/Variance Tradeoff
- Bias-Variance Tradeoff Using Python
What is Bias?
Bias can be best described as the difference between the actual prediction of our model to the correct value trying to predict. A model with high bias might pay very little attention to the training data and hence it rather oversimplifies the model. Such a model will always lead to high errors in training and test data. Bias is a phenomenon that completely skews the result of an algorithm in favor of or against an idea. Bias is considered to be a systematic error that occurs in the machine learning model automatically due to incorrect assumptions in the ML process. It depends on the quality and size of training data being used to teach it. Using faulty, poor or incomplete data will always result in inaccurate predictions, further describing the saying of “garbage in, garbage out”, telling us that the quality of the output produced is determined by the quality of the input given.
Register for our upcoming AI Conference>>
It is recommended that an algorithm should always be low biased to avoid the problem of underfitting. Due to high bias, the output from predicted data turns out to be in a straight-line format, thus not fitting accurately in the data and also the data set. Such a fitting of data is known as Underfitting. This happens when the presented hypothesis is too simple or linear in nature. Bias generally occurs due to the problems introduced by the one who trains the machine learning systems. Some Examples of low-bias machine learning algorithms are Decision Trees, k-Nearest Neighbors and Support Vector Machines and a few examples of high-bias Machine Learning algorithms include Linear Regression, Discriminant Analysis and Logistic Regression.
What is Variance?
Variance is the complete opposite of Bias. During training, the created model is allowed to inspect and search the data a certain number of times to find patterns in it. If it cannot work properly on the data for long enough, it will not find patterns and bias occurs. But if the model is allowed to search the data too many times, it will learn very well for only that particular data. It will capture most patterns in the data but will also learn from the unnecessary data present, known as the noise. We can define variance as a model’s sensitivity to fluctuations in the data. If our model learns from noise, this will cause our model to consider trivial features that are not as important. Nonlinear machine learning algorithms have a lot of flexibility and generally have a high variance.
The higher the variance of the model, the more complex the model will become and the more will it be able to learn complex functions. However, if the model is made too complex for the dataset, where a simpler solution was possible, high Variance will cause the model to overfit. Low Variance suggests small changes to the target function with changes to the training dataset. High Variance suggests large changes to the target function with changes to the training dataset. Low Variance Machine Learning algorithms include Linear Regression, Linear Discriminant Analysis and Logistic Regression. Some examples of high-variance machine learning algorithms include Decision Trees, k-Nearest Neighbors and Support Vector Machines.
The Bias-Variance Tradeoff
Bias and variance are inversely connected and It is nearly impossible practically to have an ML model with a low bias and a low variance. When we modify the ML algorithm to better fit a given data set, it will in turn lead to low bias but will increase the variance. This way, the model will fit with the data set while increasing the chances of inaccurate predictions. The same applies while creating a low variance model with a higher bias. Although it will reduce the risk of inaccurate predictions, the model will not properly match the data set. Hence it is a delicate balance between both biases and variance. But having a higher variance does not indicate a bad ML algorithm. Machine learning algorithms should be created accordingly so that they are able to handle some variance. Underfitting occurs when a model is unable to capture the underlying pattern of the data. Such models usually present with high bias and low variance.
It happens when we have very little data to build a model or when we try to build a model with linear features making use of nonlinear data. The phenomenon of Overfitting occurs when our model captures the noise along with the underlying pattern in data. It generally takes place when we train our model a lot over noisy datasets. Such models have low bias and high variance. This is the trade-off faced as is known as the tradeoff between bias and variance. An algorithm cannot be termed as more and less complex at the same time. To build a nearly perfect model, one needs to find a good balance between bias and variance present in the model so that it minimizes the total error induced. To achieve the balance between Bias error and the Variance error, we need such a value of k, that the model neither learns from the noise nor it makes blind assumptions that underfits the data. A correct balance between bias and variance will help neither overfit nor underfit the model. Therefore understanding bias and variance is a critical aspect for understanding the behavior of models especially in cases of prediction.
How to overcome Bias-Variance Tradeoff
One of the practices to reduce Bias can be to change the methodologies being used to create models. So for Models having High bias, the correct method will be not to use a Linear model if features and target variables of data do not in fact have a Linear Relationship. The correct way to tackle high variance will be to train the data using multiple models. Ensemble learning methods also help to leverage both weak and strong learners in the model to improve the model prediction. Most best-suited solutions in Machine Learning make use of Ensemble Learning. Another way can be to ensure that the training data is diverse and represents all possible groups or outcomes.
In the presence of an imbalanced dataset, using weighted or penalized models can be considered as an alternative. The most common source of error is generally due to the training dataset not being diverse in nature and hence the model being created not having enough training data to clearly identify or differentiate between a problem. Introducing more data increases the data to noise ratio which may help reduce the variance of the present model. When the model is fed with more data, it has shown to be able to come up with a better understanding of the data which is then also applied to newly introduced data points.
Bias-Variance Tradeoff Using Python
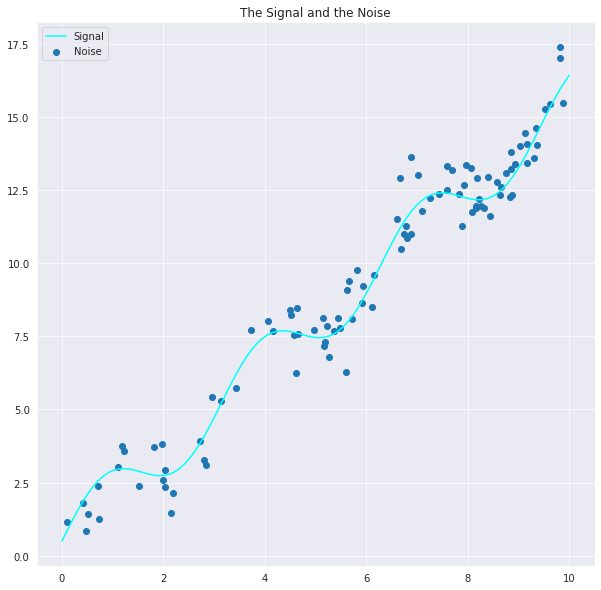
The Bias-Variance Tradeoff Problem can also be best understood practically using Python and Numpy. Below I have tried to provide a graphical understanding of the Bias-Variance Tradeoff Problem in Machine Learning. Here we will observe what happens to a model as we vary the noise generated by the data generating a signal and analyze the results.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('darkgrid')
from sklearn.linear_model import LinearRegression
# Creating signal and Plotting It
def generate_data(x, noise_threshold=0.1):
signal = np.sin(2 * x) + (1.5 * x) + 0.5
noise = np.random.normal(0, 1, size=len(x)) * noise_threshold
return signal + noise
x = np.random.uniform(0, 10, 100)
y = generate_data(x=x, noise_threshold=0.7)
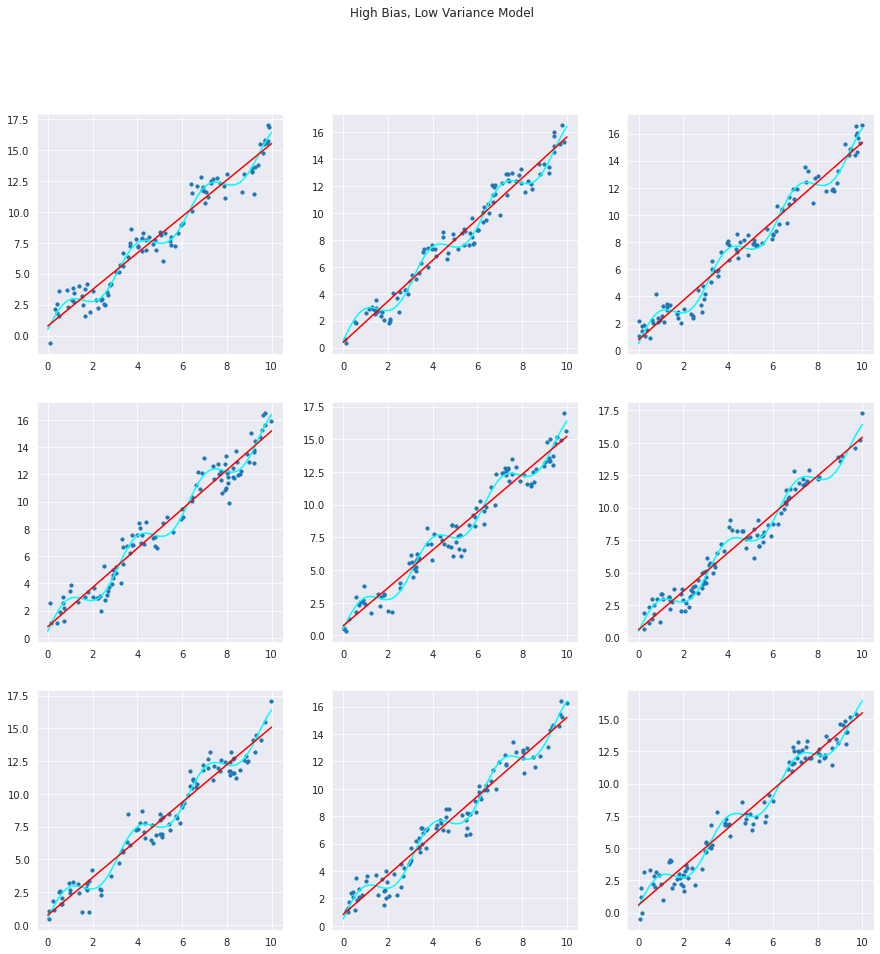
#Creating a High Bias, Low Variance Model
signal_x = np.linspace(0, 10, 100)
signal_y = generate_data(x=signal_x, noise_threshold=0.0)
plt.plot(signal_x, signal_y, color='cyan')
x = np.random.uniform(0, 10, 100)
y = generate_data(x=x, noise_threshold=0.7)
plt.scatter(x=x, y=y, s= 10)
#Creating a High Variance, Low Bias Model
signal_x = np.linspace(0, 10, 100)
signal_y = generate_data(x=signal_x, noise_threshold=0.0)
plt.plot(signal_x, signal_y, color='cyan')
x = np.random.uniform(0, 10, 100)
y = generate_data(x=x, noise_threshold=0.7)
plt.scatter(x=x, y=y, s= 10)
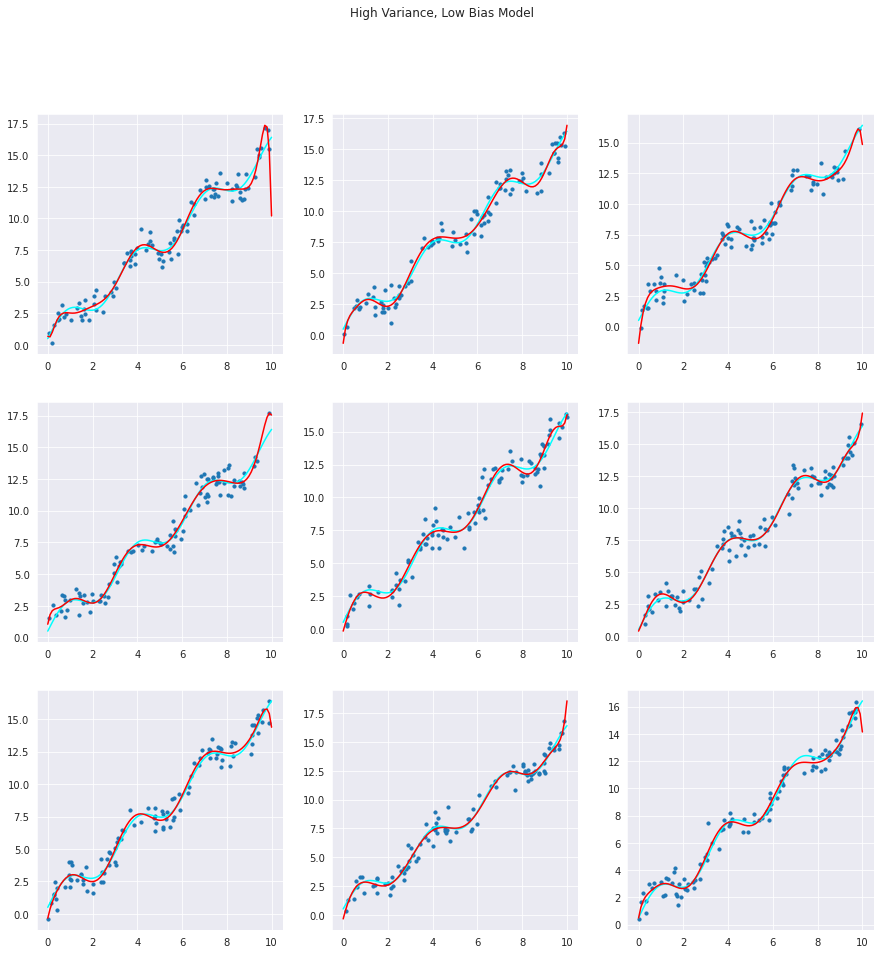
As we can observe, with changing the noise generated by the data generating signals, the levels of variance and bias also do change.
Conclusion
The Bias-Variance Tradeoff Problem is an important aspect that cannot be overlooked while building a Machine Learning algorithm or model. Addressing this issue defines the accuracy of the model and how the model performs when new and unseen data is introduced to the model. Therefore, one should aim for a near to perfect balance between the bias and variance in the model being created.
training set squared error data science irreducible error
